Помощь студентам
В разделе предложены учебно-методические публикации по ряду технических дисциплинам, приведен ряд решений графических задач
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
1N. Двойное проницание поверхности/ Метод.указания/ Винокурова Л.М., Матвеева Л.А., Чмых И.Г. - Оренбург, 2003. - 73 стр. - metod82 (962 Kb)
2N. Метрические задачи/ Метод указания/ Садовская Е.А. - Оренбург, 2003. - 17 стр. - metod159 (245 Kb)
3N. Начертательная геометрия/ Метод. указания к выполнению контрольных работ/ Воронков А.И., Васильева М.А., Иванова А.П. - Оренбург, 2003. - 28 стр. - metod95 (478 Kb)
4N. Начертательная геометрия/ Метод. указания к лабораторным работам/ Г.А. Баздеров, Е.Г. Родина. - Кемерово, 2010. - 32 стр. - 1410 (94 Kb)
5N. Начертательная геометрия для первокурсника/ Учебное пособие/ С.И. Лазарев, Э.Н. Очнев, О.А. Абоносимов. - Тамбов, 2004. - 68 стр. - Lazarev (574 Kb)
6N. Поверхности. Образование поверхностей. Развертки, сечения/ Индивидуальные задания и методические указания для самостоятельной работы студентов/ Л.Е. Бахтина, З.Г. Котельникова/ Кемерово, 2008. - 38стр. - 3746 (1 Mb)
7N. Модель плоскости на эпюре Монжа/ Методические указания к выполнению расчётно-графической работы для студентов/ Г.А. Баздеров. Кемерово, 2009. - 15 стр. - 3975 (149Kb)
8N. Азбука начертательной геометрии. Часть I/ Учебное пособие. О.А. Маркова - Нижнекамск: НХТИ (филиал) КГТУ, 2012. - 44 стр. http://www.nchti.ru/phocadownload/ucheb2/NG/azbuka.pdf
9N. Азбука начертательной геометрии. Часть II/ Учебное пособие. О.А. Маркова - Нижнекамск: ИПЦ "Гузель", 2016. - 91 стр. http://www.nchti.ru/phocadownload/Информационные_ресурсы_библиотеки_образовательной_организации/Начерт.геом/NGАzbuc2_Markova.pdf
10N. Начертательная геометрия. Натуральная величина плоской фигуры/ Метод. указания. О.А. Маркова - Нижнекамск: НХТИ (филиал) КГТУ, 2009. - 17 стр. http://www.nchti.ru/phocadownload/ucheb2/NG/plosk_figura.pdf
11N. Начертательная геометрия. Точки, прямые, плоскости/ Учебное пособие. О.А. Маркова. - Нижнекамск: НХТИ (филиал) КГТУ, 2013. - 132 стр. http://www.oamarkova.ru/skan/
12N. Начертательная геометрия. Методические указания к практическим занятиям для студентов технического направления заочной формы обучения / О.А. Маркова. - ИПЦ "Гузель", 2016. - 35 с. http://www.nchti.ru/phocadownload/Информационные_ресурсы_библиотеки_образовательной_организации/Начерт.геом/NGmetod2016_Markova.pdf
13N. Тесты по начертательной геометрии/ Сборник тестовых заданий. О.А. Маркова - Нижнекамск: ИПЦ "Гузель", 2016. - 61 стр. http://www.nchti.ru/phocadownload/Информационные_ресурсы_библиотеки_образовательной_организации/Начерт.геом/NG-testiMarkova.pdf
14N. Решение задач по начертательной геометрии. Учебно-методическое пособие / О.А. Маркова. - Нижнекамск: ИПЦ «Гузель», 2018. - 86 с. http://www.nchti.ru/phocadownload/Информационные_ресурсы_библиотеки_образовательной_организации/Начерт.геом/NGReshenie_Markova.pdf
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ и ИНЖЕНЕРНАЯ ГРАФИКА
1NG. Инженерная графика. Часть 1/ Метод. указания и контрольная работа №1 для студентов заочной формы обучения/ Мищенко Н.П. - Новосибирск, 1998. - 1,75 п.л. - ig1 (223 Kb)
2NG. Учебная программа дисциплины "Начертательная геометрия. Инженерная графика" / К.А. Вольхин/ Новосибирск, 2009. - 52 стр. - UP (2 Mb)
3NG. Инженерная графика. Начертательная геометрия. Часть I. Контрольные задания для студентов-заочников технических специальностей высших учебных заведений/ Метод. указания. О.А. Маркова - Нижнекамск: НХТИ (филиал) КГТУ, 2012. - 44 стр. http://www.nchti.ru/phocadownload/ucheb2/NG/metod.pdf
ИНЖЕНЕРНАЯ ГРАФИКА
1G. Неразъемные соединения/ Метод. указания/ Припадчев А.Д. - Оренбург, 2003. - 40 стр. - metod357 (857 Kb)
2G. Инженерная графика. Альбом заданий для выполнения сборочных чертежей/ Учебное пособие/ Столер В.А., Резанко А.А., Мисько М.В. - БГУИР - 140 стр. - metodichka po cbor (1,2 Mb)
3G. Инженерная графика. Эскизирование деталей сборочного узла. Выполнение сборочного чертежа узла/ Метод.указания/ Подоплелов Е.В., Лукьянова Н.В., Устюгова Н.А. - Ангарск, 2008. - 24 стр. - eskiz (5,8 Mb)
4G. Геометрическое черчение/ Вялков В.И./ Методическое указание. - metodichka (299 Kb)
5G. Инженерная графика. Часть I/ Учебное пособие. О.А. Маркова - Нижнекамск: Нижнекамский химико-технологический институт (филиал) ФГБОУ ВПО "КНИТУ", 2012. - 83 стр. http://www.nchti.ru/phocadownload/ucheb2/Inj_graf/Inj_graf1.pdf
6G. Инженерная графика. Часть II/ Учебное пособие. О.А. Маркова - Нижнекамск: Нижнекамский химико-технологический институт (филиал) ФГБОУ ВПО "КНИТУ", 2012. - 92 стр. http://www.nchti.ru/phocadownload/ucheb2/Inj_graf/Inj_graf2.pdf
7G. Тесты по инженерной графике/ Сборник тестовых заданий. О.А. Маркова - Нижнекамск: ИПЦ "Гузель", 2017. - 64 стр. http://www.nchti.ru/phocadownload/Информационные_ресурсы_библиотеки_образовательной_организации/Инж_гр/IG-testiMarkova.pdf
8G. Инженерная графика. Сопряжение/ Учебно-метод. пособие. О.А. Маркова. - Нижнекамск: Нижнекамский химико-технологический институт (филиал) ФГБОУ ВПО "КНИТУ", 2013. - 90 стр. http://www.nchti.ru/phocadownload/ucheb2/Inj_graf/Sopryazh.pdf
9G. Инженерная графика. Нанесение размеров/ Метод. указания. О.А. Маркова. - Нижнекамск: Нижнекамский химико-технологический институт (филиал) ФГБОУ ВПО "КНИТУ", 2013. - 50 стр. http://www.nchti.ru/phocadownload/ucheb2/Inj_graf/razmeri.pdf
КОМПЬЮТЕРНАЯ ГРАФИКА
1K. Компьютерная графика в системе КОМПАС-3D LT 5.11/ Учебное пособие/ Шутов Д.А. - Иваново, 2006. - 64 стр. - cg(525 Kb)
2К. Основные этапы разработки чертежа и создание сборок (блоков в системе AutoCAD 2000/ Диванова О.П. - Череповец, 2003. -113 стр. - etap_autocad (16 Mb)
ПРИКЛАДНАЯ МЕХАНИКА
1PM. Детали машин/ Учебно-метод. пособие/ Ю.В. Воробьев, А.Д. Ковергин, Ю.В. Родионов, П.А. Галкин. - Тамбов, 2004. - 96 стр. - DM (2 Mb)
2PM. Проектирование винтового механизма/ Расчетно-пояснительная записка к курсовому проекту по деталям машин. - 12 стр. - 10259 (52Kb)
3PM. ПРИКЛАДНАЯ МЕХАНИКА. Теория машин и механизмов: Учебное пособие/ О.А. Маркова. - Нижнекамск: Нижнекамский химико-технологический институт (филиал) ФГБОУ ВПО «КНИТУ», 2013. - 80 с. http://www.nchti.ru/phocadownload/ucheb2/prikl_mech/ucheb2.pdf
4PM. ПРИКЛАДНАЯ МЕХАНИКА. Детали машин. Часть I: Учебное пособие/ О.А. Маркова. - Нижнекамск: Нижнекамский химико-технологический институт (филиал) ФГБОУ ВПО «КНИТУ», 2013. - 123 с. http://www.nchti.ru/phocadownload/ucheb2/prikl_mech/ucheb.pdf
Файлы найдены на просторах Интернета....
ГРАФИЧЕСКИЕ ПРИМЕРЫ
Некоторые материалы раздела заимствованны со следующих сайтов: ru.wikipedia.org; www.l1574.ru/RESOURCE/ks; lib.qrz.ru; sumdu.telesweet.net и др...
Линия пересечения двух плоскостей общего положения:
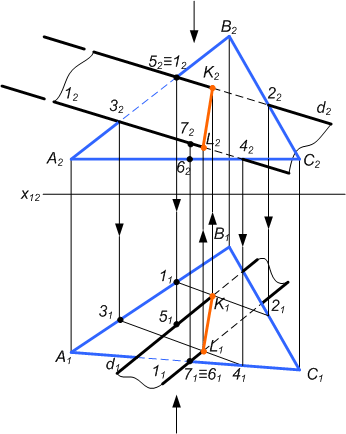 В предлагаемом примере плоскость Т задана треугольником АВС, а плоскость Р - двумя параллельными прямыми d и l. Для решения этой задачи достаточно определить две точки, которые одновременно принадлежат обеим плоскостям. В приведенном примере такими точками являются точки K и L. Таким образом, KL -линия взаимного пересечения заданных плоскостей. Тчк К найдена как точка пересечения прямой d, которая принадлежит плоскости Р, с плоскостью Т, заданной треугольником АВС (K=d∩T(ΔABC)). Точка L найдена как точка пересечения прямой l, принадлежащей плоскости Р, с плоскостью Т, заданной треугольником АВС(L=l∩T(ΔABC)). Заключительным этапом решения задач на взаимное пересечение плоскостей является определение взаимной видимости частей плоскости относительно друг друга. Для определения взаимной видимости используют конкурирующие точки - 1 и 5, 7 и 6.
В предлагаемом примере плоскость Т задана треугольником АВС, а плоскость Р - двумя параллельными прямыми d и l. Для решения этой задачи достаточно определить две точки, которые одновременно принадлежат обеим плоскостям. В приведенном примере такими точками являются точки K и L. Таким образом, KL -линия взаимного пересечения заданных плоскостей. Тчк К найдена как точка пересечения прямой d, которая принадлежит плоскости Р, с плоскостью Т, заданной треугольником АВС (K=d∩T(ΔABC)). Точка L найдена как точка пересечения прямой l, принадлежащей плоскости Р, с плоскостью Т, заданной треугольником АВС(L=l∩T(ΔABC)). Заключительным этапом решения задач на взаимное пересечение плоскостей является определение взаимной видимости частей плоскости относительно друг друга. Для определения взаимной видимости используют конкурирующие точки - 1 и 5, 7 и 6.
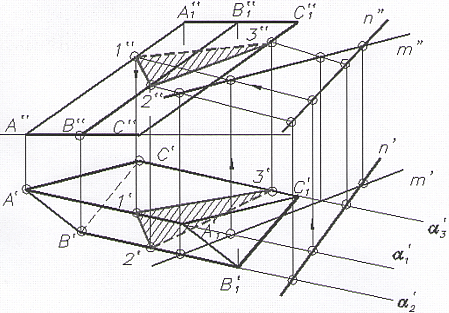
Пересечение плоскости общего положения (задана прямыми m ∩ n) с призмой:
Для построения линии пересечения необходимо использовать вспомогательные секущие плоскости, которые совмещают с ребрами поверхности. На рис. показано построение точки 1, находящейся на ребре AA1, через которое проведена вспомогательная секущая плоскость α1.
Пересечение пирамиды SABC плоскостью общего положения α:
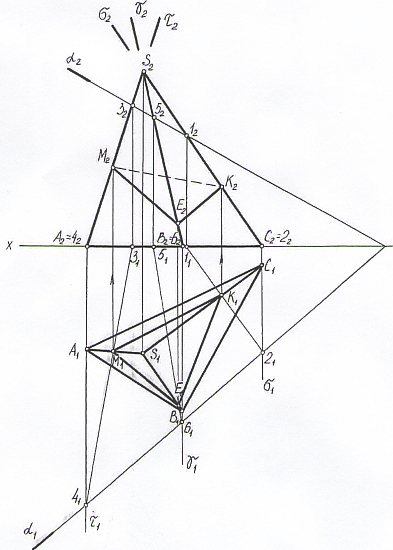 Основание пирамиды лежит в плоскости π1 и плоскостью α не пересекается. При решении задачи через ребра пирамиды проведены вспомогательные фронтально проецирующие плоскости: S2C2 ≡ σ2, S2B2 ≡ γ2, S2A2 ≡ τ2. Точка К определена на пересечение ребра SC с плоскостью α, при этом через прямую SC проведена вспомогательная фронтально-проецирующая плоскость σ. Эта плоскость пересекла плоскость α по линии 1-2. В свою очередь 1-2 пересекла ребро SA в точке К. Тчк К принадлежит линии пересечения пирамиды с плоскостью α. Тчк Е определяем с помощью вспомогательной плоскости, проходящей через ребро SB, а тчк М - с помощью вспомогательной плоскости, проходящей через ребра SA. Δ ЕМК представляет собой линию пересечения пирамиды SABC с плоскостью α (α1, α2). Видимость сторон Δ-ка ЕМК определяется по принадлежности видимым и невидимым граням пирамиды, плоскость α считается прозрачной.
Основание пирамиды лежит в плоскости π1 и плоскостью α не пересекается. При решении задачи через ребра пирамиды проведены вспомогательные фронтально проецирующие плоскости: S2C2 ≡ σ2, S2B2 ≡ γ2, S2A2 ≡ τ2. Точка К определена на пересечение ребра SC с плоскостью α, при этом через прямую SC проведена вспомогательная фронтально-проецирующая плоскость σ. Эта плоскость пересекла плоскость α по линии 1-2. В свою очередь 1-2 пересекла ребро SA в точке К. Тчк К принадлежит линии пересечения пирамиды с плоскостью α. Тчк Е определяем с помощью вспомогательной плоскости, проходящей через ребро SB, а тчк М - с помощью вспомогательной плоскости, проходящей через ребра SA. Δ ЕМК представляет собой линию пересечения пирамиды SABC с плоскостью α (α1, α2). Видимость сторон Δ-ка ЕМК определяется по принадлежности видимым и невидимым граням пирамиды, плоскость α считается прозрачной.
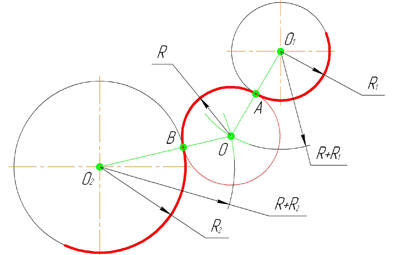
Сопряжение дуг с дугами
При внешнем сопряжении центры О1 и О2 сопрягаемых дуг радиусов R1 и R2 лежат вне сопрягающей дуги радиуса R. Внешнее сопряжение дуг выполняется в следующей последовательности: 1) Находим центр сопряжения, точку О пересечения дуг окружностей с радиусами R1+R и R2+R соответственно концентричных окружностям с радиусами R1 и R2; 2) Соединяем прямыми центр сопряжения О с центрами окружностей О1 и О2, которые пересекаясь с заданными окружностями определяют положение точек сопряжения А и В; 3) Строим сопряжение:
Как начертить эллипс?
Эллипс (греч. elleipsis - недостаток) - линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и пересекающей все прямолинейные образующие одной полости этого конуса.Эллипс - множество точек М плоскости (рис.1), сумма расстояний r1= МF1 и r2= МF2 которых до двух определенных точек F1(-c,0) и F2(c,0) этой плоскости (фокусов эллипса) постоянна - r1+r2=2а. Середина 0 отрезка F1F2 (фокусного расстояния) называется центром эллипса.
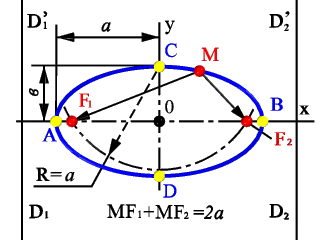 Рис.1
Рис.1
В прямоугольной системе координат 0ху с началом в центре эллипса, на оси 0х которой лежат фокусы эллипса уравнение эллипса имеет следующий вид - х2/а2+у2/в2=1, в2=а2-с2, где а и в - длинны большой и малой полуосей эллипса. При а=в фокусы F1 и F2 совпадают и указанное уравнение определяет окружность, которая рассматривается как частный случай эллипса.
Эллипс - центральная линия второго порядка. Эллипс - замкнутая линия, симметричная относительно осей 0x и 0y главных (большой и малой) осей и центра.
В курсе инженерной графики эллипсы встречаются наиболее часто в трех случаях: 1)сечение конуса плоскостью пересекающей ось конуса; 2)сечение циллиндра наклонной плоскостью; 3)изображение окружностей в аксонометрических проекциях (построение изометрической или диметрической проекций).
Методик построения эллипсов несколько, рассмотрим только одну из них. Возьмем окружность диаметром 30мм. Такая окружность в изометрии будет иметь вид эллипса с осями 36,6мм и 21,3 мм (Рис.2).
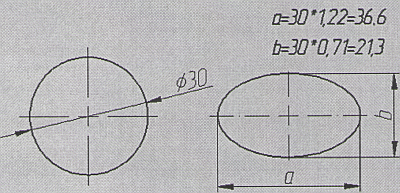 Рис.2
Рис.2
На первом этапе необходимо из центра эллипса провести две вспомогательные окружности, диаметры которых будут равны большой и малой оси эллипса. Затем, из центра проведем несколько лучей, так чтоб они пересекали обе окружности. Для удобства отображения будем рассматривать одну четверть. Количество вспомогательных лучей зависит исключительно от желаемой точности построений и размеров эллипса, в нашем случае это будут 3 луча (рекомендованное количество лучей для эллипсов с большой осью от 60 до 120 мм) (Рис.3). Следующим шагом получим дополнительные точки эллипса. Для этого, поочередно делаем с каждым лучем следующее: из точки пересечения луча с малой окружностью проведем горизонтальную линию в сторону большой окружности, а из точки пересечения луча с большой окружостью проведем линию до пересечения с только что начерченной горизонталью. Таким образом получим точки 2, 3 и 4. Точки 1 и 5 так же принадлежат эллипсу (Рис.4).
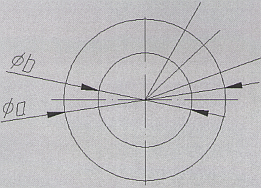
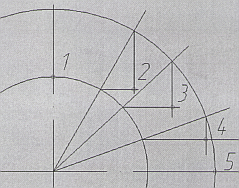
Рис.3 Рис.4
Имея пять точек без труда проведем через них кривую. Внимание: в точке пересечения с осями кривая эллипса строго перпендикулярна им (Рис.5). Осталось достроить оставшиеся три четверти фигуры. Можно воспроизвоести построения по аналогии, тем самым, доведя умение построения до навыка. Второй варивнт построения - просто отразить точки 2, 3, 4 через оси (Рис.6).
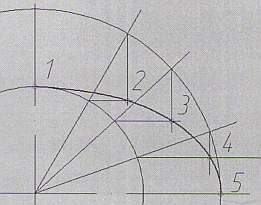
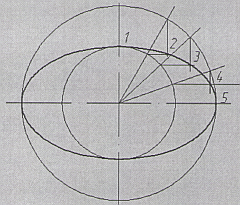
Рис. 5 Рис. 6
Как начертить изометрию?
Изометрическая проекция — аксонометрическая проекция, при которой длины единичных отрезков на всех трёх осях одинаковы. Применяется в машиностроительном черчении для отображения внешнего вида детали, а также в компьютерной графике.
В вашей детали может быть большое количество построений, но основные принципы останутся неизменными.Начнем с того, что определимся с направлением осей в изометрии (рис.1).
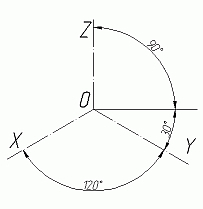
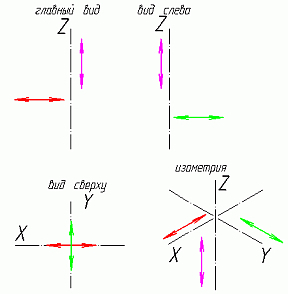
На следующей схеме (Рис.2) показано соответствие направлений, по которым откладываются размеры в изометрии по отношению к размерам на чертеже. Возьмем для примера не сложную деталь. Это параллелепипед 50х60х80мм, имеющий сквозное вертикальное отверстие диаметром 20 мм и сквозное прямоугольное отверстие 50х30мм (Рис.3).Начнем построение изометрии с вычерчивания верхней грани фигуры. Расчертим на требуемой нам высоте тонкими линиями оси Х и У. Из получившегося центра отложим вдоль оси Х 25 мм (половина от 50) и через эту точку проведем отрезок паралллельный оси У длиной 60 мм. Отложим по осиУ 30 мм (половина от 60) и через полученную точку проведем отрезок параллельный оси Х длиной 50 мм. Достроим фигуру(Рис.4).
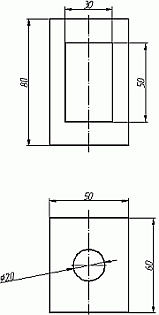
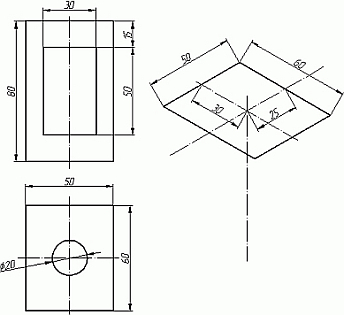
Рис.3 Рис.4
Мы получили верхнюю грань фигуры. Не хватает только отверстия диаметром 20 мм. Построим это отверстие. В изометрии окружность изображается особым образом - в виде эллипса. Это связано с тем, что мы смотрим на нее под углом. В изометрии окружности проецируются в эллипсы с размерами осей a=1,22D и b=0,71D. Эллипсы, обозначающие окружности на горизонтальных плоскостях в изометрии изображаются с осью а расположенной горизонтально, а ось b - вертикально. При этом расстояние между точками расположенными на оси Х или У равно диаметру окружности (смотри размер 20 мм) (Рис.5).
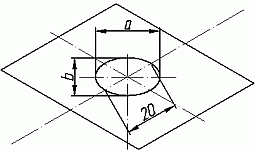 Рис.5
Рис.5
Теперь, из трех углов нашей верхней грани начертим вниз вертикальные ребра - по 80 мм и соединим их в нижних точках. Фигура почти полностью начерчена - не хватает только прямоугольного сквозного отверстия (Рис.6). Чтобы начертить его опустим вспомогательный отрезок 15 мм из центра ребра верхней грани (указан голубым цветом). Через полученную точку проводим отрезок 30 мм параллельный верхней грани (и оси Х). Из крайних точек чертим вертикальные ребра отверстия - по 50 мм. Замыкаем снизу и проводим внутреннее ребро отверстия, оно параллельно оси У (Рис.7).
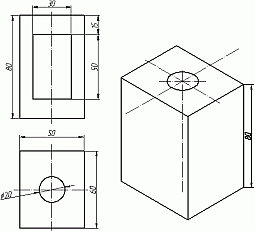
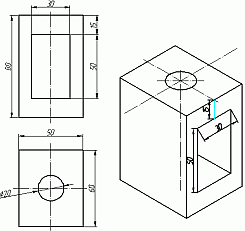
Рис.6 Рис.7
На этом простая изометрическая проекция может считаться завершенной. Как правило, в курсе инженерной графики выполняется изометрия с вырезом одной четверти. Чаще всего, это четверть нижняя левая на виде сверху - в этом случае получается наиболее интересный с точки зрения наблюдателя разрез. На нашем примере эта четверть обозначена красными линиями. Удалим ее (Рис.8)
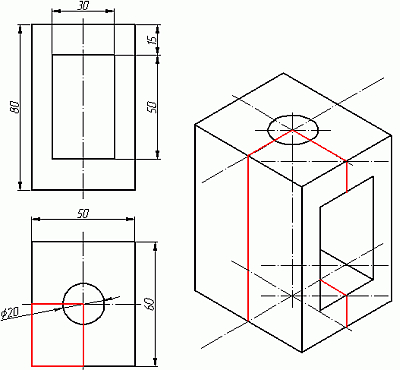 . Рис.8
. Рис.8
Как видим из получившегося чертежа, сечения полностью повторяют контур разрезов на видах (смотри соответствие плоскостей обозначенных цифрой 1), но при этом они вычерчены параллельно изометрическим осям. Сечение же второй плоскостью повторяет разрез выполненный на виде слева (в данном примере этот вид мы не чертили) (Рис.9).
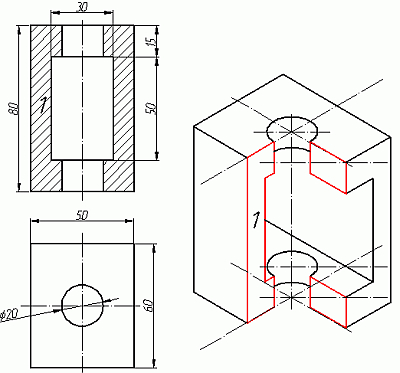 Рис.9
Рис.9
Осталось заштриховать плоскости сечений, но с этим, я думаю, вы справитесь сами...
Построение наглядного изображения предмета
Для построения наглядного изображения предмета воспользуемся аксонометрическими проекциями. Выполнить изображение можно по его комплексному чертежу - рис.1. Построим стандартную прямоугольную изометрию, воспользуемся приведенными коэффициентами искажения. Примем расположение начала координат (точка О) – в центре нижнего основания предмета (рис.2). Вычертив оси изометрии и установив масштаб изображения (аксонометрия-1.22:1), отмечаем центры окружностей верхнего и нижнего оснований цилиндра, а также окружностей, ограничивающих Т-образный вырез. Вычерчиваем эллипсы, являющиеся изометрией окружностей. Затем проводим линии, параллельные координатным осям, которые ограничивают вырез в цилиндре. Изометрию линии пересечения сквозного цилиндрического отверстия, ось которого параллельна оси Оу с поверхностью основного цилиндра, строим по отдельным точкам, используя те же точки (К, L, М и им симметричные), что и при построении вида слева. Затем удаляем вспомогательные линии и обводим окончательно изображение с учетом видимости отдельных частей предмета (Рис.3).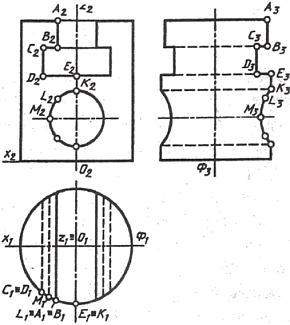
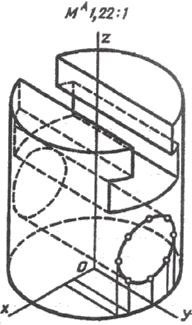
Рис.1 Рис.2
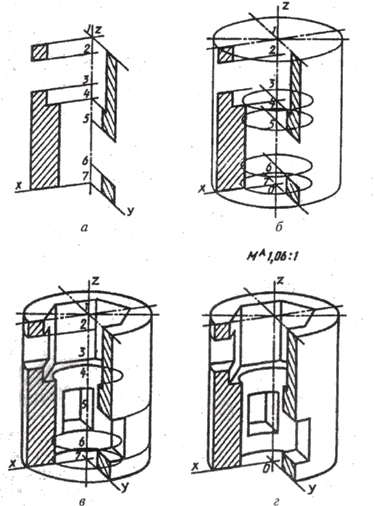 Рис.3
Рис.3